Estrategias de Matemáticas SAT

Para ser dueño de la sección de matemáticas del SAT, necesita algunas estrategias. Bueno, los tenemos. Desde cuántas preguntas hay en la sección de matemáticas del SAT hasta estrategias tangibles para abordar las preguntas, lea, marque e imprima la publicación a continuación para su próxima sesión de estudio.

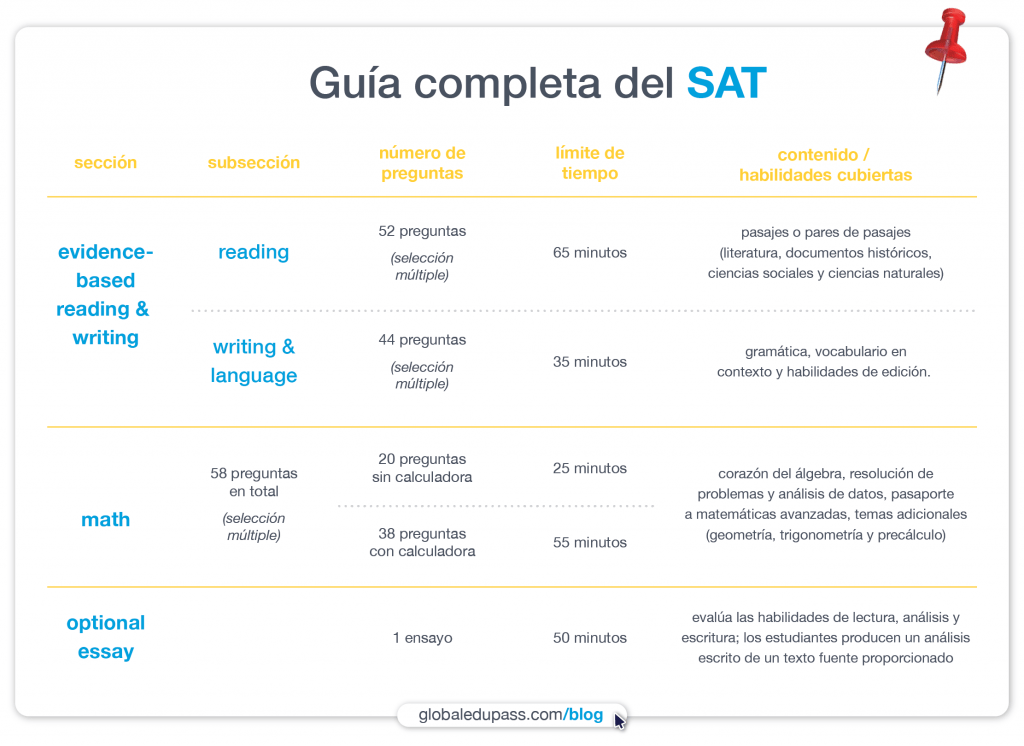
Primero, una descripción general rápida de la sección de matemáticas del SAT

Tendrá 80 minutos en total para completar 58 preguntas.

Comenzará con la parte Sin calculadora, donde resolverá 20 preguntas en 25 minutos. De estas 20 preguntas, las primeras 15 son de opción múltiple y las últimas 5 son respuestas elaboradas por los estudiantes.

Una vez transcurridos esos 25 minutos, se le permitirá sacar su calculadora para completar las 38 preguntas restantes. Tendrá 55 minutos para esta parte. De estas 38 preguntas, sí, lo adivinaste, algunas son no opción multiple. Los primeros 30 serán de opción múltiple y los 8 restantes serán respuestas cuadriculadas producidas por los estudiantes.

¿Qué son las respuestas producidas por los estudiantes?

No se proporcionan opciones de respuesta para aproximadamente el 20% de las preguntas. Ustedes tienen que pensar en una respuesta y cuadricularla como una fracción o un decimal. La buena noticia es que solo hay cuatro dígitos/espacios, por lo que la elección de la respuesta debe ser relativamente simple, sin soluciones locas y complicadas.

¿Qué, sin calculadora? ¡No hay problema!

Algo que intimida a algunos estudiantes del SAT es que hay una parte en la que no poder utiliza una calculadora. Esto es diferente del ACT que permite el uso de una calculadora en toda la sección de matemáticas. Sin embargo, no tema, porque descubrirá que rara vez necesita su calculadora para cualquier parte de la prueba, incluso cuando se le permite usarla. ¡Eso es correcto! Si está intentando resolver un problema y los números parecen demasiado difíciles de manipular sin una calculadora, entonces necesita repensar su estrategia. Debe haber una forma más sencilla.

Para obtener información sobre los temas tratados en el SAT, consulte el final de esta publicación. Por ahora, ¡concentremos nuestra atención en la estrategia!

Estrategias de tiempo

Márcalo y saltéalo

Como dijimos, tendrá 25 minutos para responder los primeros 20 problemas sin calculadora y 55 minutos para responder los 38 problemas con calculadora, por lo que no querrá dedicar demasiado tiempo a ningún problema. No deje que una pregunta lo desconcierte por mucho tiempo antes de márcalo, sáltatelo y sigue adelante. También puede marcar las preguntas que respondió pero no estaba seguro de haber respondido correctamente. Asegúrese de tener un reloj o de poder ver el reloj porque realmente necesita llevar la cuenta del tiempo.

Regrese a sus preguntas sin respuesta o inseguras cuando le queden solo unos minutos en esa parte. No puede volver a la parte sin calculadora una vez que haya comenzado la parte con calculadora, por lo que debe asegurarse de haber respondido todo en la primera parte en los primeros 25 minutos. No hay penalización por respuestas incorrectas.; en cambio, recibe crédito por cada pregunta que responde correctamente, así que no dejes ninguna respuesta en blanco.

Saltar a las preguntas cuadriculadas

En la mayoría de las pruebas estandarizadas, las preguntas se vuelven más difíciles a medida que avanza hacia el final; sin embargo, hay una advertencia para el SAT: las últimas dos preguntas de opción múltiple en cada porción probablemente será difícil, mientras que el primer par de respuestas cuadriculadas producidas por los estudiantes debería ser fácil, pero seguramente sería difícil adivinar una respuesta a una pregunta cuadriculada cuando no puede elegir solo A, B, C o D como lo haces para la opción múltiple.

Por lo tanto, no dedique demasiado tiempo a las últimas dos preguntas de opción múltiple en cada parte porque necesita llegar a esas preguntas cuadriculadas. En su lugar, omita las preguntas de opción múltiple que consumen mucho tiempo, responda las preguntas de respuesta producidas por los estudiantes (al menos las primeras dos más fáciles), luego regrese y haga una suposición informada sobre esas preguntas difíciles de opción múltiple que le estaban tomando demasiado tiempo. .

Si encuentra que tiene un poco de tiempo extra, vuelva a esos problemas de los que no estaba seguro y revíselos, pero no los haga como lo hizo la primera vez. En su lugar, pruebe otra estrategia o ingrese su respuesta y vea si funciona.

Resolver rápidamente (pero con precisión)

Necesitas usar tu razonamiento para tratar de encontrar el más rápido manera de resolver cada problema. Si bien se le permite una calculadora para un porción del SAT de matemáticas, todos los problemas se pueden resolver sin uno y, con frecuencia, la ruta más rápida no implica el uso de una calculadora. Asegúrese de estar familiarizado con la calculadora que trae a la prueba (y que sea una que esté aceptada para su uso) y sepa cuándo usarla y cuándo seguramente podrá trabajar más rápido sin ella. De hecho, cada problema está escrito para que pueda resolverse sin una calculadora, por lo que es mejor que reserve su calculadora para cuando regrese a verificar las respuestas.

En general, las preguntas de la sección de matemáticas del SAT se vuelven más difíciles a medida que avanzas hacia el final de cada parte de la prueba (con la excepción de que cambia de opción múltiple a una grilla creada por los estudiantes, como se mencionó anteriormente). Esto significa dos cosas. Primero, le gustaría tener más tiempo para los problemas más desafiantes al final, pero segundo, realmente quiere asegurarse de pasar suficiente tiempo para responder correctamente las primeras preguntas. Necesita resolver esos problemas más fáciles correctamente, así que muévase rápido, pero no tan rápido como para cometer errores por descuido.

Además, a diferencia del ACT, el SAT sí te da una hoja de fórmulas. Esta hoja de referencia es generalmente solo para preguntas de geometría. Probablemente ya conozca esta información, pero se proporciona por si acaso. Debe familiarizarse con él solo para saber lo que se proporciona. Si una pregunta usa una fórmula inusual que no se espera que sepa, esa fórmula estará presente en la pregunta. Hay algunas fórmulas que se espera que conozcas, y otras que seguramente te facilitarían mucho el examen si las conocieras. Consulte nuestra guía de estudio Fórmulas para la sección de matemáticas del SAT aquí.

Consejos de estudio para la sección de matemáticas del SAT

Haz una prueba cronometrada de práctica

Para imitar mejor el proceso que usará cuando tome el SAT real, imprima una prueba de práctica y una hoja de respuestas, configure un cronómetro de 25 minutos para la primera parte (sin calculadora) y comience a resolver problemas. Si no termina, continúe y termine las preguntas restantes, pero marque que necesitó tiempo adicional. Luego haz lo mismo con la parte de la calculadora (55 minutos).

Identifique sus debilidades y aprenda de ellas

Una vez que haya completado su prueba de práctica, verifique sus respuestas. De los que te perdiste, realmente deberías buscar un par de cosas:

Uno, ¿hay patrones en tus errores? ¿Te faltan preguntas de geometría, preguntas abstractas o preguntas con muchas palabras? ¿Tuviste problemas con las preguntas cuadriculadas producidas por los estudiantes? ¿Necesitabas tiempo extra? ¿Qué puedes hacer para acelerar tu proceso? Identifica tus debilidades.

Dos, cuando verifique sus respuestas, trate de averiguar qué hizo mal. No diga simplemente: «Oh, me perdí esas ocho preguntas». ¡Descubre cómo hacerlos! Envuelva su cerebro alrededor del problema. Vea si puede averiguar cómo hacerlo incluso antes de mirar la explicación. Y luego, intente con otra pregunta similar (siempre puede cambiar los números para escribir un nuevo problema para usted).

Todo esto se llama «metacognición», que simplemente significa «pensar en tu propio pensamiento». Si no analizas tus errores, puedes hacer todas las pruebas de práctica del mundo, pero seguirás cometiendo los mismos errores. La práctica NO hace la perfección. ¡La práctica perfecta hace la perfección!

hacer más problemas; Ataque con estrategia y propósito

Debido a que necesita moverse rápidamente, considere cómo aborda cada problema. Esta no es una prueba como la que tomas en la escuela secundaria donde el maestro te dice que no obtendrás crédito si no lo haces de la manera que él o ella quiere. Haz lo que funcione para ti, pero ten en cuenta que deberían esté anotando, dibujando y probando números, buscando patrones, escribiendo ecuaciones algebraicas y básicamente escupiendo sus ideas en papel. ¿Qué tipo de estrategias podría probar?

Estrategias de resolución de problemas para SAT Math

Dibuja una imagen

Algunas preguntas son abstractas y un bosquejo rápido puede ayudarlo a «ver» lo que está preguntando el problema.

Ejemplo: Un cubo tiene 2 caras pintadas de rojo y las caras restantes pintadas de azul. El área total de las caras rojas es de 32 cm.². ¿Cuál es el volumen del cubo en centímetros cúbicos?

Dibuja un bosquejo rápido del cubo y marca lo que sabes para que puedas ver lo que pide el problema.

Oh, cada cara roja debe tener un área de 16 cm cuadrados por lo que cada lado debe ser de 4 cm. El Volumen debe ser 4 x 4x 4 o 64 cm cúbicos.

Números de complemento

¿Las variables te deprimieron? A veces, las variables hacen que el problema parezca más difícil de lo que realmente es. Trate de sustituir números (y elija números «inteligentes» que faciliten el problema) y vea si puede manipular el problema de esa manera.

Ejemplo: Cuando el entero positivo norte se divide por 9el resto es 7. ¿Cuál es el resto cuando n+3 se divide por 9?

Prueba con un número. A ver, ¿qué número podría dividirse por 9 y dejar un resto de 7? Bueno, 16 dividido por 9 es 1 y el resto sería 7. Entonces, ¿cuál es el resto de 16+3 dividido por 9?

Haz una tabla o lista y busca un patrón

No tiene que ser hermoso, pero debe estar lo suficientemente organizado para que sepa lo que quiere decir y lo que está buscando.

Ejemplo: Cada término en una secuencia aritmética determinada es siempre mayor que el que le precede, y la diferencia entre dos números consecutivos es siempre la misma. Si los términos 3 y 5 son 19 y 79, ¿cuál es el término 7?

¡Ajá, la secuencia suma 30 cada vez!

«Actuarlo

Obviamente, no puede simplemente pararse en la sala de pruebas y comenzar a mover las cosas, sino que esencialmente puede «actuar» un problema anotando las cosas en un papel.

Ejemplo: un salón de clases tiene 8 mesas con capacidad para 4 personas. Si 26 estudiantes están sentados en las mesas y ninguna de las mesas está vacía, ¿cuál es el mayor número posible de mesas en las que están sentadas 4 personas?

Usar lógica

No haga conjeturas aleatorias, al menos hágalas lógicas.

Ejemplo: en el plano de coordenadas xy, las líneas s y t son perpendiculares. Línea s pasa por el origen y contiene el punto (-2,-1). La línea t también contiene el punto (-2,-1) y punto (0, n). ¿Cuál es el valor de norte?

Si las opciones de respuesta son A) -5 B) -3 C) -2 D) 2 E) 3 entonces un bosquejo muy rápido muestra que la respuesta no puede ser positiva. Al menos use su lógica aquí y elimine las malas opciones de respuesta.

No hagas el problema más difícil de lo que es

Asegúrate de responder el problema que se te pide. No haga pasos que son innecesarios.

Ejemplo: si (2x-8)(2x+8)=36, ¿cuál es el valor de 4×2?

(2x-8)(2x+8)=36

4×2-64=36

4 × 2 = 100 ¡Deténgase aquí! No es necesario resolver para x. No pierda su tiempo con pasos adicionales. Note lo que la pregunta estaba haciendo.

Conceptos que puede esperar que se cubran en el examen

Su informe de puntaje SAT incluirá su puntaje en la sección de Matemáticas, que varía de 200 a 800, así como tres subpuntajes que muestran cómo se desempeñó en tres categorías: corazón de álgebra, Resolución de problemas y análisis de datosy Pasaporte a Matemáticas Avanzadas.

Nota: Los temas adicionales de Matemáticas contribuyen a la puntuación total, pero no se notifican como subpuntuación.

Para el corazón de álgebra preguntas (aproximadamente el 33% del total de preguntas) es posible que deba:

• Encuentra la distancia en una recta numérica, entre puntos en un plano de coordenadas o en términos de valor absoluto
• Use la traducción de palabras a símbolos y ecuaciones lineales y desigualdades para resolver problemas del mundo real en contexto
• Manipular y evaluar expresiones y ecuaciones variables (incluido el valor absoluto)
• Resolver desigualdades lineales y cuadráticas y relacionarlas con las gráficas correspondientes
• Encuentra e interpreta pendientes e intersecciones de ecuaciones, problemas verbales y gráficos (también usando propiedades de líneas paralelas y perpendiculares)
• Emparejar, interpretar y analizar información de gráficos en el plano de coordenadas
• Resolver e interpretar sistemas de ecuaciones lineales y desigualdades lineales tanto en el contexto de problemas del mundo real como sin contexto

Para Resolución de problemas y análisis de datos conceptos (aproximadamente el 29% del total de preguntas) necesitará:

• Resolver problemas de varios pasos usando razones, proporciones, tasas, porcentajes y/o conversión de unidades de medida
• Consultar datos, cuadros, tablas de frecuencia y gráficos para interpretar la información.
• Demostrar conocimiento de medidas de tendencia central y distribución (media, mediana, moda, rango), cómo calcular cada una y cómo calcular un punto de datos faltante dada una medida de tendencia central
• Calcular probabilidades de un evento, su complemento y combinaciones (probabilidad condicional y conjunta) en contexto
• Demostrar conocimiento del principio fundamental de conteo y diagramas de Venn
• Comprender los fundamentos de las estadísticas (muestreo aleatorio, distribución, desviación estándar, intervalo de confianza e interpretación de resultados)
• Interpretar características clave y relaciones entre variables en gráficos
• Comprender las diferencias entre relaciones lineales, cuadráticas y exponenciales en contexto (frecuentemente como interés simple y compuesto o crecimiento/decaimiento)
• Ampliar patrones, tanto aritméticos como geométricos, aumentando y disminuyendo por factores o proporciones comunes

Pasaporte a Matemáticas Avanzadas conceptos (aproximadamente el 28% del total de preguntas) pueden poner a prueba su capacidad para:

• Manipular exponentes en potencias de 10 y notación científica, y aplicar propiedades de exponentes racionales
• Demostrar conocimiento del sistema de números reales: números racionales, irracionales y complejos
• Sumar, restar, multiplicar y dividir polinomios
• Crear e interpretar funciones cuadráticas o exponenciales en contexto
• Analizar, resolver y graficar ecuaciones y sistemas cuadráticos u otros no lineales
• Manipular expresiones y ecuaciones con exponentes, enteros y potencias racionales, radicales y fracciones con variables en el denominador
• Interpretar y evaluar funciones y funciones compuestas
• Interpretar funciones y sus gráficas.
  • Identifica intersecciones y valores máximos y mínimos
  • Encontrar dominio y rango y asíntotas
  • Comprender el aumento y la disminución, el comportamiento final y las transformaciones/traducciones
• Escribir funciones que sean directa o inversamente proporcionales o exponenciales

Temas Adicionales en Matemáticas preguntas (aproximadamente el 10% del total de preguntas) con frecuencia combinar múltiples conceptos de geometría en una pregunta en contexto. Estos conceptos incluyen su capacidad para:

• Calcule longitudes y puntos medios de segmentos de línea (segmentos superpuestos y aquellos en el plano de coordenadas)
• Calcular perímetro y área de polígonos y circunferencia y área de círculos
• Usar propiedades de líneas paralelas, otras propiedades de ángulos y figuras y proporciones similares para encontrar medidas de ángulos faltantes o longitudes/distancias de lados
• Usar las propiedades de los triángulos isósceles y rectángulos para calcular longitudes de lados desconocidas y medidas de ángulos (simetría, teorema de Pitágoras, etc.)
• Demostrar conocimiento de triángulos rectángulos (30^o60^o90^o; 45^o45^o90^o) y aplicar razones trigonométricas (seno, coseno, tangente) para resolver los valores faltantes
• Manipular entre área, volumen y área de superficie
• Comprender la trigonometría del círculo unitario y las identidades trigonométricas básicas para resolver problemas relacionados con radianes y medidas de ángulos.
• Comprender las relaciones de los círculos, como los ángulos centrales e inscritos, la longitud del arco y el área del sector, las tangentes y las cuerdas.
• Crea la ecuación de un círculo en el plano de coordenadas encontrando el centro y el radio
• Manipular (sumar, restar, multiplicar, dividir, simplificar) números complejos (i=-1)

Ahora que está armado con el tiempo y las estrategias de resolución de problemas, y el conocimiento del contenido de la prueba, ¡está listo para entrenar para el maratón de matemáticas que es la sección de matemáticas del SAT! Puede encontrar cientos de problemas de práctica con explicaciones que le enseñan los conceptos que necesita saber en el curso SAT de Olive Book. Simplemente visite soysat.com para inscribirse.